Contents

Ha & Eck (2017) | A Neural Representation of Sketch Drawings (sketch-rnn)

Ha and Eck used the drawings collected from users of Google’s “Quick, Draw!” game to train a Sequence-to-Sequence Variational Autoencoder (VAE) on the sketches. The sketches are represented as simple sequence of straight-line strokes (polylines) and do not use the SVG format. The VAE consists of encoder and decoder. The encoder is a bidirectional RNN. The decoder is an autoregressive RNN that samples output sketches conditional on a given latent vector.

Available resources at a glance

sketchrnn paper

Fig. 27 Screenshot of the sketchrnn paper

Use cases

The trained model allows for a range of simple use cases:

  • Conditional reconstruction

  • Latent Space Interpolation, i.e. generate drawings between two encoded latent vectors

  • Sketch drawing analogies, i.e. latent vector arithmetic, e.g. \(\text{cat head} + (\text{complete pig} - \text{pig head}) = \text{complete cat}\)

  • Predicting different endings of incomplete sketchs / sketch auto-complete

Latent Space Interpolation

sketchrnn Latent Space Interpolation

Fig. 28 Screenshot of Latent Space Interpolation from the sketchrnn paper

The trained model allows for a latent space interpolation, as shown in the figure above. However, the interpolation may not result in a visual that is semantically meaningful if the latent space positions correspond to different concepts.

However, if the latent space positions correspond to the same concept, the linear interpolation allows for the generation of interesting and useful results, as shown below in case of the interpolation between four reproduced sketches of a human head / face.

The bottom row shows the four (reproduced) sketches that were used as starting points for the linear interpolation.

sketchrnn Latent Space Interpolation - starting points- Heads

Fig. 29 Screenshot of Latent Space Interpolation from the sketchrnn paper;

You can find them again in the four corners of the image below.

sketchrnn Latent Space Interpolation - Heads

Fig. 30 Screenshot of Latent Space Interpolation from the sketchrnn paper;

Latent vector arithmetics (analogies)

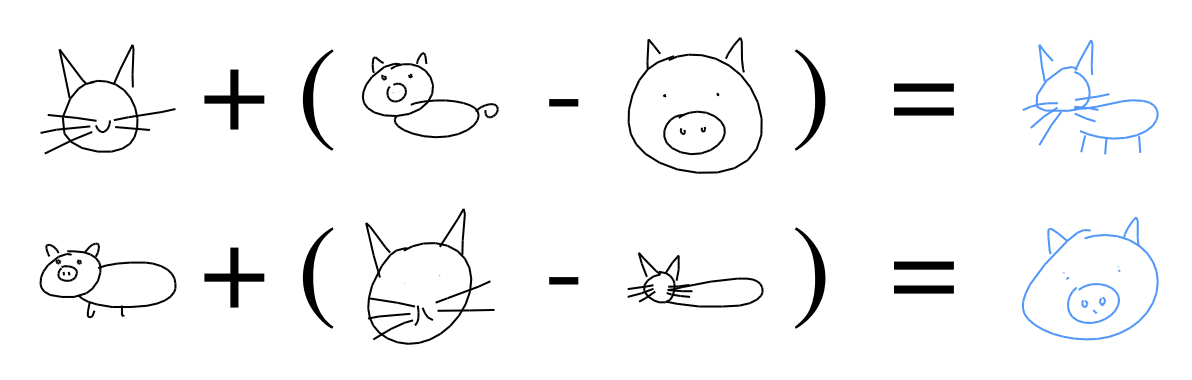
sketchrnn Latent Space Interpolation

Fig. 31 Screenshot of Latent Space Interpolation from the sketchrnn paper

Similar to the famous NLP example of king/queen and male/female vectors, it was possible to perform basic arithmetics in embedding space, as shown in the figure above.

Data representation

Sketches are represented as a sequence of pen stroke actions. Each sketch consists of a list of “points”. Each point is then represented by a 5-dimensional feature vector: \((\Delta x, \Delta y, p_1, p_2, p_3)\). The parameters \(p_1\) to \(p_3\) are a binary one-hot encoding of three possible states of the “pen”.

  1. \(\Delta\) x – the offset distance in the x direction

  2. \(\Delta\) y – the offset distance in the y direction

  3. \(p_1\) – pen is currently touching the paper and line will be drawn connecting the next point with the current point (1) or not (0)

  4. \(p_2\) – pen will be lifted from the paper after the current point and no line will be drawn next (1) or not (0)

  5. \(p_3\) – drawing has ended and subsequent points (incl. the current one) will not be rendered (1) or not(0)

The initial absolute coordinate of the drawing is assumed to be located at the origin (0, 0).

Limitations of the data representation

Using this data representation, a sketch can only consist of a sequence of straight lines. However, the sample rate at which the mouse cursor position is obtained allows for curves and circles.

Overall limitations:

  • Each drawing consists of a sequence of straight lines.

  • No abstract shapes, like circles, rectangles

  • No curves (like Bézier curves) or circle segments

Model architecture of “sketch-rnn”

The overall model is a Sequence-to-Sequence Variational Autoencoder (VAE).

Encoder (from input to latent vector)

The encoder is a bidirectional RNN that takes a sketch as an input, and outputs a latent vector. Since the RNN is bidirectional it if fed the sketch sequence in normal as well as in reversed order. Two encoding RNNs make up the bidirectional RNN and two final hidden states are obtained. Both concatenated form the overall hidden state.

Decoder (from latent vector to output)

Our decoder is an autoregressive RNN that samples output sketches conditional on a given latent vector.