Carlier et al. (2020) | DeepSVG: A Hierarchical Generative Network for Vector Graphics Animation¶
Available resources at a glance
This paper was accepted to the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada.
Fig. 39 Screenshot of the DeepSVG paper¶
Data representation¶
Mental model and the paper’s nomenclature¶
The figure below attempts to illustrate the DeepSVG mental model and nomenclature.
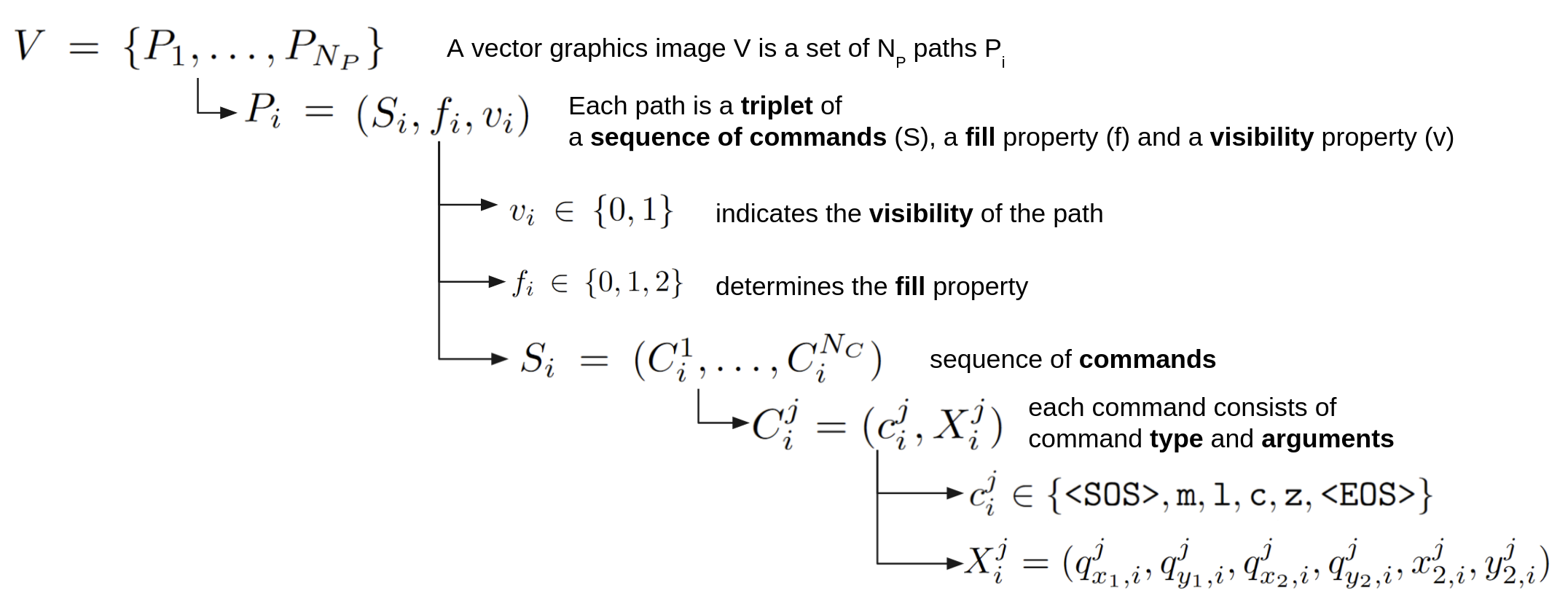
Fig. 40 Own illustration using the definitions and formulae from the DeepSVG paper¶
Path encoding example¶
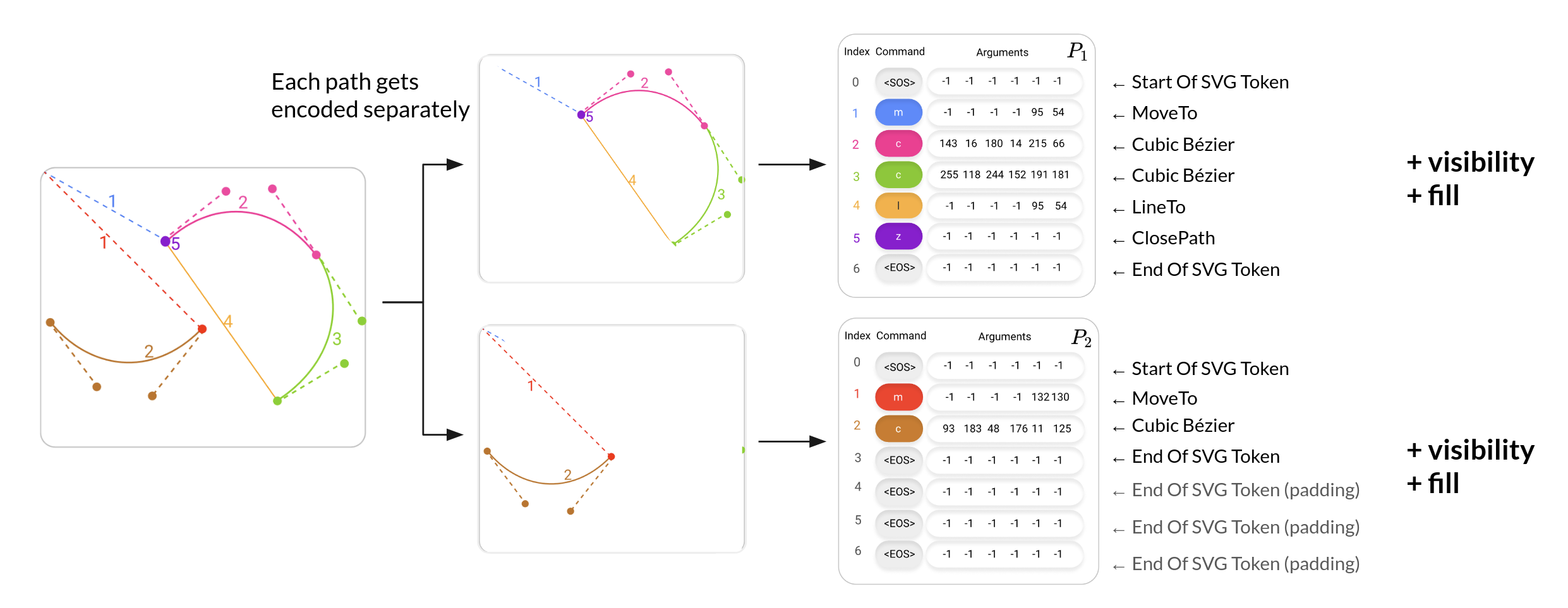
Fig. 41 Visualisation of how SVG paths are encoded to a tensor in DeepSVG; visualisation by the author re-using figures from the DeepSVG paper¶
The figure above shows two separate paths:
Two cubic Bézier curve segments and a closing straight line described by: Blue(1) \(\rightarrow\) Pink(2) \(\rightarrow\) Green(3) \(\rightarrow\) Yellow(4) \(\rightarrow\) Violet(5)
A single cubic Bézier curve segment described by: Red(1) \(\rightarrow\) Brown(2)
Each of these paths get encoded separately. The path encoding consists of a sequence of commands and arguments plus a visibility and a fill flag.
Data preprocessing¶
Prior to DeepSVG preprocessing: Minified SVGs need special treatment¶
Please note that a treatment of SVGs using a tool, such as SVGO, may be required. DeepSVG cannot deal with minified SVGs where commands and parameters are not clearly separated by commas or whitespace.
See Chapter Data Representation > Common preprocessing for details.
Preprocessing within DeepSVG¶
Open questions:
What about layers?
What about groups?
…
1. Converting relative to absolute commands¶
All commands in the path data of an SVG are converted from relative to absolute commands. This is more than just converting the command letters from lower case to upper case. The command parameters also need to be converted.
2. Decomposition: Converting basic SVG shapes to paths¶
There are 6 basic SVG shapes:
<circle><ellipse><line><polygon><polyline><rect>
These can be decomposed and converted into paths without any visually perceivable loss.
Open question
Is it possible to keep these basic SVG shapes as part of the feature vector? Would this help with ensuring that circles remain circles and are not just approximated by squiggly lines in the SVG output?
Unsupported basic SVG shape |
Explanation |
Replacement |
|---|---|---|
A circle defined by the center point (x,y) and a radius. |
Transformed to a path using four Elliptical Arc commands, which themselves are converted to Cubic Bézier curves. |
|
An ellipse defined by 4 parameters, the ellipses position (x,y) and the radius on the x axis and the radius on the y axis |
Transformed to a path using four Elliptical Arc commands, which themselves are converted to Cubic Bézier curves. |
|
A straight line defined by the start point (x1, y1) and the end point (x2, y2) |
Converted into a path using the LineTo command |
|
A closed shape consisting of a set of connected straight line segments. A polygon is defined by a sequence of points; the last point is connected to the first point. |
Converted into a path using the LineTo command. |
|
A shape consisting of a sequence of connected traight line segments. As opposed to the |
Converted into a path using the LineTo command. |
|
A rectangle defined by position (x, y), their width and height (and optionally the radius for rounded corners) |
Converted into a path using the LineTo command. Please note that DeepSVG may overlook the option of rounded corners at this point. |
Decomposition of circles¶
DeepSVG implements a decomposition using 4 elliptical arcs. The example from the paper is a circle defined as follows:
<circle
cx="1"
cy="1"
r="1"
/>
So, this is a circle around the center point \((1, 1)\) with a radius of 1 (and, thus, a width of 2). This circle gets translated a MoveTo command and four elliptical arc curves followed by a closing command.
<path
d="
M1,0
A1,1 0 0 1 2,1
A1,1 0 0 1 1,2
A1,1 0 0 1 0,1
A1,1 0 0 1 1,0
z
"
/>
The first arc starts at the top point of the circle (remember that \(y=0\) is the top in the SVG coordinate system) and draws a quarter circle in a clockwise direction to the absolute point \((2, 1)\).
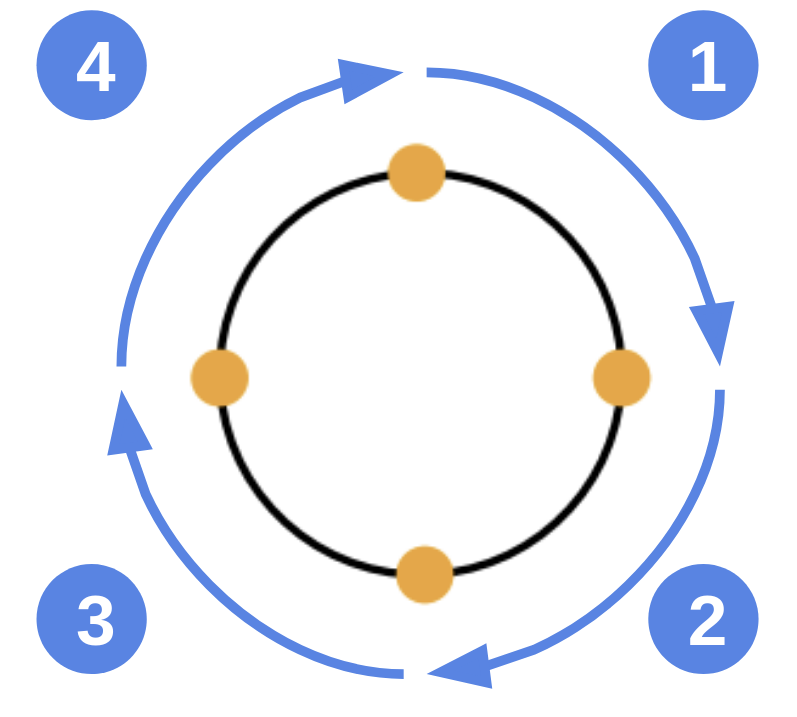
Fig. 42 Circle decomposition in DeepSVG using four elliptical arc curves; center figure from Appendix of the DeepSVG paper¶
3. Converting commands that are not M, L, C, Z¶
All path commands that are not part of the subset supported by DeepSVG are converted and represented by commands from the supported subset.
The supported subset is:
These commands have been chosen deliberately as the other SVG commands can be represented or at least approximated using these basic commands.
Not directly supported commands are: { VerticalLineTo V; HorizontalLineTo H; SmoothCubicBezier S; Quadratic Bézier Curve Q; Smooth Quadratic Bezier T; Elliptical Arc Curve A }. These commands are replaced by others.
Carlier et al. also add two commands that just denote the start and end of the SVG:
<SOS>– start of the SVG token<EOS>– end of the SVG token; this command is also used for padding to fill up the sequence of commands up to the permitted maximum number of commands.
All arguments of these two additional commands are always equal to -1.
Unsupported commands |
Explanation |
Replacement |
|---|---|---|
This is just a simple way of defining a vertical line. LineTo is the general commands for all types of straight lines and can also represent vertical lines. |
LineTo L |
|
This is just a simple way of defining a horizontal line. LineTo is the general commands for all types of straight lines and can also represent horizontal lines. |
LineTo L |
|
This is just a simple way of defining a smooth cubic bézier curve. The cubic bézier C is the general commands for all types of cubic bézier curves and can also represent smooth cubic béziers. |
Cubic Bézier Curve C |
|
Higher-order cubic bézier curves can also represent quadratic bézier curves |
Cubic Bézier Curve C |
|
This is just a simple way of defining a smooth quadratic bézier curve. The cubic bézier C can also represent all quadratic, including smooth quadratic béziers. |
Cubic Bézier Curve C |
|
Elliptical arc curves are curves defined as a portion of an ellipse. |
Converted to Cubic Bézier curves which can approximate the elliptical arc. |
4. Path simplification¶
To simplify the neural network’s task of representation learning, paths are simplified. Generally, the aim is to reduce the number of points that form a shape. But, in some instances, the number of points can increase if the resolution of a curve would otherwise be too low.
Simplification approach¶
If the SVG input only consisted of smooth curves, the simplification step could simply be to reparametrize points on that curve so that they are placed equidistantly from one another. However, since SVG shapes contain sharp angles and, thus, corners, these points should not be changed. Consequently, the simplification is done in two steps:
Split paths at points that form a sharp angle.
This is measured by the angle between the incoming and the outcoming tangent
If the angle is smaller than some threshold \(\eta = 150°\), then the angle is considered sharp
Apply a simplification algorithm to the resulting shapes
For line segments: Ramer-Douglas-Peucker algorithm (from “Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or its Caricature” (1973)); the same algorithm was also used by Ha and Eck (2017)
For segments of cubic Bézier curves: Philip J. Schneider algorithm (from “An Algorithm for Automatically Fitting Digitized Curves” (1990))
The resulting lines and Bézier curves are divided in multiple subsegments if their length is larger than some distance \(\Delta = 5\).
Open question
Are these segments connected again later? Or do they remain split?
This could be a stupid question. The paths get just divided in the path data. They likely remain connected.
Simplification examples & discussion¶
The following simplification examples were shared in the paper:
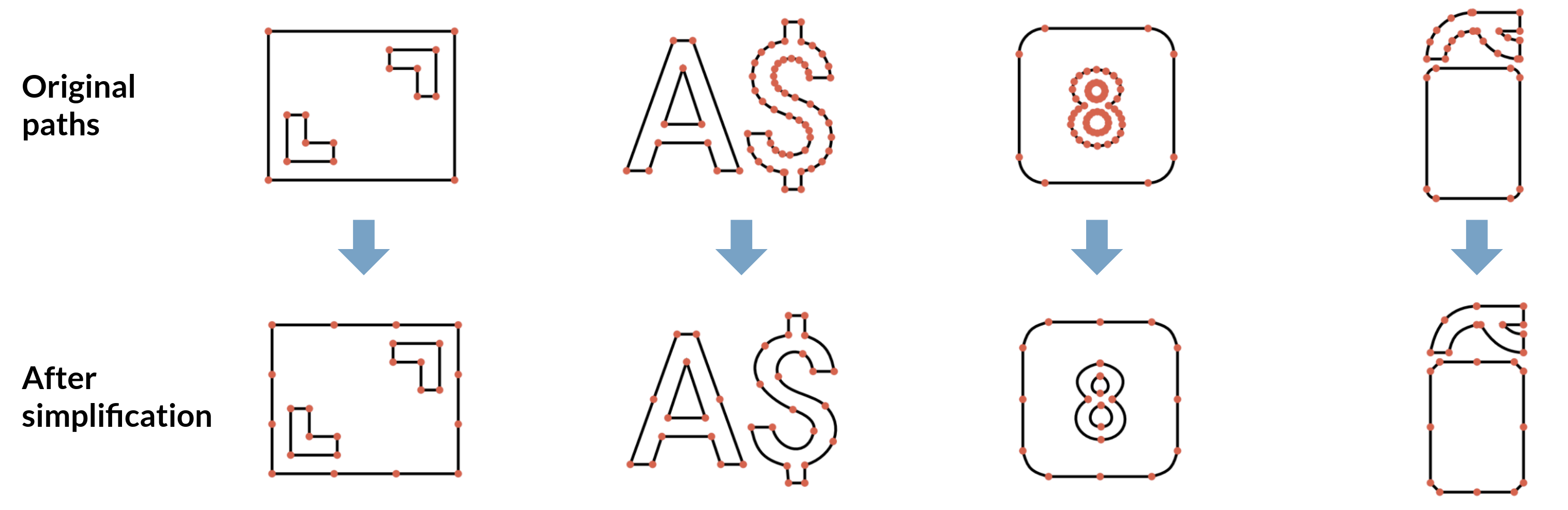
Fig. 43 DeepSVG simplification examples; examples taken from the DeepSVG paper; added descriptions and arrows for clarity¶
A number of observations can be made at this point (you may need to click on the figure above to see the enlarged image and to make these observations for yourself):
The Simplification may also add points
Counterintuitively, the simplification step can add points if the resolution in the original is too low.
This is indeed the case in all four examples, e.g.:
This is the case in the first example from the left: The outer rectangle gains 8 points through the simplification step.
This is also the case in the third example from the left: The rectangle with rounded corners gains 4 points through the simplification step.
As desired, corner points do not get removed and the overall appearance of the shape is maintained.
The fidelity of the simplification is suboptimal
The counter spaces (inner spaces) of the number 8 in the third example were perfect or near-perfect circles before. After the simplification step, they are much higher than they are wide, nearly forming a corner at the top.
The bottom of the Dollar sign in the second example has a rectangular shape in the original with 90° angles. After the simplification step, the left previously vertical line is now tilted to the left.
In the fourth example, the bottom shape is a rectangle with rounded corners. However, after the simplification step, these rounded corners have been replaced by straight lines.
Open question
What parts of the simplification process cause which aspects of the observed suboptimal fidelity? Are there some easy workarounds? Any errors introduced into the training examples through the preprocessing will never get corrected by the neural network (unless by pure chance). Since we are in full control of the preprocessing it seems somewhat negligent to permit these visually perceptible errors.
5. SVG normalization¶
The following SVG normalization steps are carried out:
Paths are canonicalized, that is, any shapes starting position is chosen to be the topmost leftmost point and the commands are oriented clockwise
All SVGs are scaled to a **normalized viewbox of size 256 x 256.
This step is called “numericalize” within the DeepSVG code and can be found in
dataset.preprocesswheresvg.numericalize(256)is
If dataset.simplify is called, the following three steps are executed:
svg.canonicalize(normalize=normalize)svg.simplify_heuristic()svg.normalize()
Embedding¶
Note
TODO
Model architecture¶

Fig. 44 DeepSVG model architecture; figure taken from the DeepSVG paper¶
Reproducing results & critical discussion¶
The DeepSVG paper is incredibly inspiring and the work that was done by Alexandre within the scope of just his Master’s thesis is truly amazing. Alexandre was kind enough to have a long video call with the author and then also helped with various follow-up questions.
Caveat: It is possible that the results shown below are result of a misunderstanding of how to correctly apply DeepSVG and not necessarily a weakness inherent to DeepSVG.
Open question
What is the maximum number of groups permitted? Reports of crashes with more than 8 groups.
Squiggly, sketchy outputs for unknown reason¶
It was possible to train a DeepSVG model and use it to generate SVG output. However, it was not possible to reproduce high-quality SVGs: When applied to a training dataset of SVG icons, the results generated by DeepSVG were often somewhat squiggly and looked more like sketches than an accurate icon. The figure below shows a selection of some of the better results.

Fig. 45 Screenshot of the author’s attempts to apply DeepSVG to a training dataset of icons¶
To better understand the source of the problem, the author applied DeepSVG to a specially designed training dataset. The author chose two (later: three) classes:
a simple perfect circle using the SVG tag
<circle>a simple perfect square using the SVG tag
<rect>(a simple five-pointed perfect star)
For each class, 1,000 identical copies of the SVG file were placed in a folder. The SVGs used <circle> and <rect> and needed to be converted into paths first. This was done via preprocessing with SVGO.
The pre-processed SVGs looked indistinguishable from the original SVG files.
DeepSVG was trained for ca. 500 epochs, i.e. more than enough for (a desired) overfitting on the examples which were identical anyways.
The results, shown in the figure below for two and three classes, appear to indicate a general problem with DeepSVG.
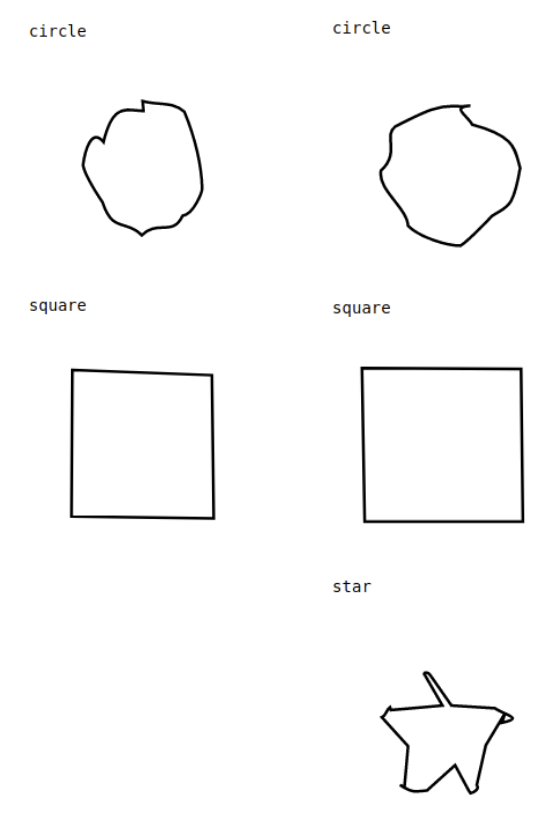
Fig. 46 Screenshot of the author’s attempts to apply DeepSVG to a training dataset of 1,000 identical icons in two (later: three) classes: circle, square, star¶
The square gets reproduced most accurately – but never with 90° angles. Generated circles and the stars are of surprisingly poor quality. The DeepSVG-internal simplification step may be a potential reason for some of these issues.
Open question
What exactly causes DeepSVG to produce squiggly output even if all the input examples of a class are simple shapes and completely identical? How could this be resolved? If solved, maybe the same DeepSVG could produce significantly better results.
Code for fill property was lost¶
Unfortunately, the code for using the fill property was lost and would need to be re-implemented. Alexandre outlined how to implement this part to the author.
Various preprocessing limitations¶
The SVG format is very complex and it is not surprising that various corner cases cannot be handled by DeepSVG. Among those are:
The rx and ry attributes of rectangles are not considered. These attributes define rounded corners.
transforms are not applied to the paths but ignored(?)
<g>(group) tags with transforms get ignored instead of applying transforms to the contained elementsmissing viewBox attribute cannot be dealt with
This is a common problems for SVGs found on the Web since SVGO used to remove the attribute by default if width and height were provided
viewBox attributes with negative starting points can cause issues
Lacking check if there are multiple svg tags in the same file
defs are ignored
css styles are not moved into affected elements
…
[TODO: Check if code was adopted from https://github.com/regebro/svg.path/blob/master/src/svg/path/path.py]